Real world tidy interest rate swap pricing
In this post I will show how easy is to price a portfolio of swaps leveraging the purrr package and given the swap pricing functions that we introduced in a previous post. I will do this in a “real world” environment hence using real market data as per the last 14th of April.
Import the discount factors from Bloomberg
Let’s start the pricing of the swap portfolio with purrr by loading from an external source the EUR discount factor curve. My source is Bloomberg and in particular the SWPM page, which allows all the Bloomberg users to price interest rate sensitive instruments. It also contains a tab with the curve information, which is the source of my curve. It is partly represented in the screenshot below and also as per the following table.

today <- lubridate::ymd(20190414)
ir_curve <- readr::read_csv(here::here("csv/Basket of IRS/Curve at 140419.csv"))
ir_curve %>%
knitr::kable(caption = "Input from Bloomberg", "html") %>%
kableExtra::kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive")) %>%
kableExtra::scroll_box(width = "750px", height = "200px")| Maturity Date | Market Rate | Shift (bp) | Shifted Rate | Zero Rate | Discount | Source |
|---|---|---|---|---|---|---|
| 04/15/2019 | -0.364000 | 0 | -0.364000 | -0.3640000 | 1.0000000 | CASH |
| 04/23/2019 | -0.378000 | 0 | -0.378000 | -0.3780000 | 1.0000735 | CASH |
| 05/16/2019 | -0.367000 | 0 | -0.367000 | -0.3670000 | 1.0003059 | CASH |
| 07/16/2019 | -0.310000 | 0 | -0.310000 | -0.3100000 | 1.0007842 | CASH |
| 10/16/2019 | -0.232000 | 0 | -0.232000 | -0.2320000 | 1.0011807 | CASH |
| 04/16/2020 | -0.227000 | 0 | -0.227000 | -0.2293661 | 1.0023373 | FRA |
| 10/16/2020 | -0.191000 | 0 | -0.191000 | -0.2164290 | 1.0033115 | FRA |
| 04/16/2021 | -0.199250 | 0 | -0.199250 | -0.1992838 | 1.0039976 | SWAP |
| 04/19/2022 | -0.130500 | 0 | -0.130500 | -0.1306045 | 1.0039393 | SWAP |
| 04/17/2023 | -0.039750 | 0 | -0.039750 | -0.0398284 | 1.0015958 | SWAP |
| 04/16/2024 | 0.055250 | 0 | 0.055250 | 0.0554430 | 0.9972325 | SWAP |
| 04/16/2025 | 0.154250 | 0 | 0.154250 | 0.1550852 | 0.9907452 | SWAP |
| 04/16/2026 | 0.256500 | 0 | 0.256500 | 0.2584914 | 0.9820912 | SWAP |
| 04/16/2027 | 0.357250 | 0 | 0.357250 | 0.3609696 | 0.9715859 | SWAP |
| 04/18/2028 | 0.458250 | 0 | 0.458250 | 0.4644039 | 0.9591332 | SWAP |
| 04/16/2029 | 0.552400 | 0 | 0.552400 | 0.5615329 | 0.9455427 | SWAP |
| 04/16/2030 | 0.638500 | 0 | 0.638500 | 0.6510037 | 0.9311096 | SWAP |
| 04/16/2031 | 0.716500 | 0 | 0.716500 | 0.7326481 | 0.9161298 | SWAP |
| 04/17/2034 | 0.901000 | 0 | 0.901000 | 0.9281277 | 0.8705738 | SWAP |
| 04/18/2039 | 1.071000 | 0 | 1.071000 | 1.1106319 | 0.8017461 | SWAP |
| 04/19/2044 | 1.134000 | 0 | 1.134000 | 1.1759181 | 0.7464983 | SWAP |
| 04/20/2049 | 1.152000 | 0 | 1.152000 | 1.1905737 | 0.7010373 | SWAP |
| 04/16/2054 | 1.150000 | 0 | 1.150000 | 1.1826028 | 0.6626670 | SWAP |
| 04/16/2059 | 1.140249 | 0 | 1.140249 | 1.1661657 | 0.6289098 | SWAP |
| 04/16/2064 | 1.131000 | 0 | 1.131000 | 1.1512813 | 0.5974307 | SWAP |
| 04/16/2069 | 1.120999 | 0 | 1.120999 | 1.1359681 | 0.5684840 | SWAP |
We now wrangle this data in order to get a two columns tibble containing the time to maturity and the discount factors for each pillar points on the curve. We us a 30/360 day count convention because it is the standard for the EUR swaps.
df.table <- ir_curve %>%
dplyr::mutate(`Maturity Date` = lubridate::mdy(`Maturity Date`)) %>%
dplyr::rowwise(.) %>%
dplyr::mutate(t2m = RQuantLib::yearFraction(today, `Maturity Date`, 6)) %>%
na.omit %>%
dplyr::select(t2m, Discount) %>%
dplyr::rename(df = Discount) %>%
dplyr::ungroup(.) %>%
dplyr::bind_rows(c(t2m = 0,df = 1)) %>%
dplyr::arrange(t2m)
ggplot2::ggplot(df.table, ggplot2::aes(x = t2m, y = df)) +
ggplot2::geom_point() +
ggplot2::geom_line(colour = "blue") +
ggplot2::ggtitle("Discount Factor curve at 14th of April 2019") +
ggplot2::xlab("Time to maturity") +
ggplot2::ylab("Discount Factor")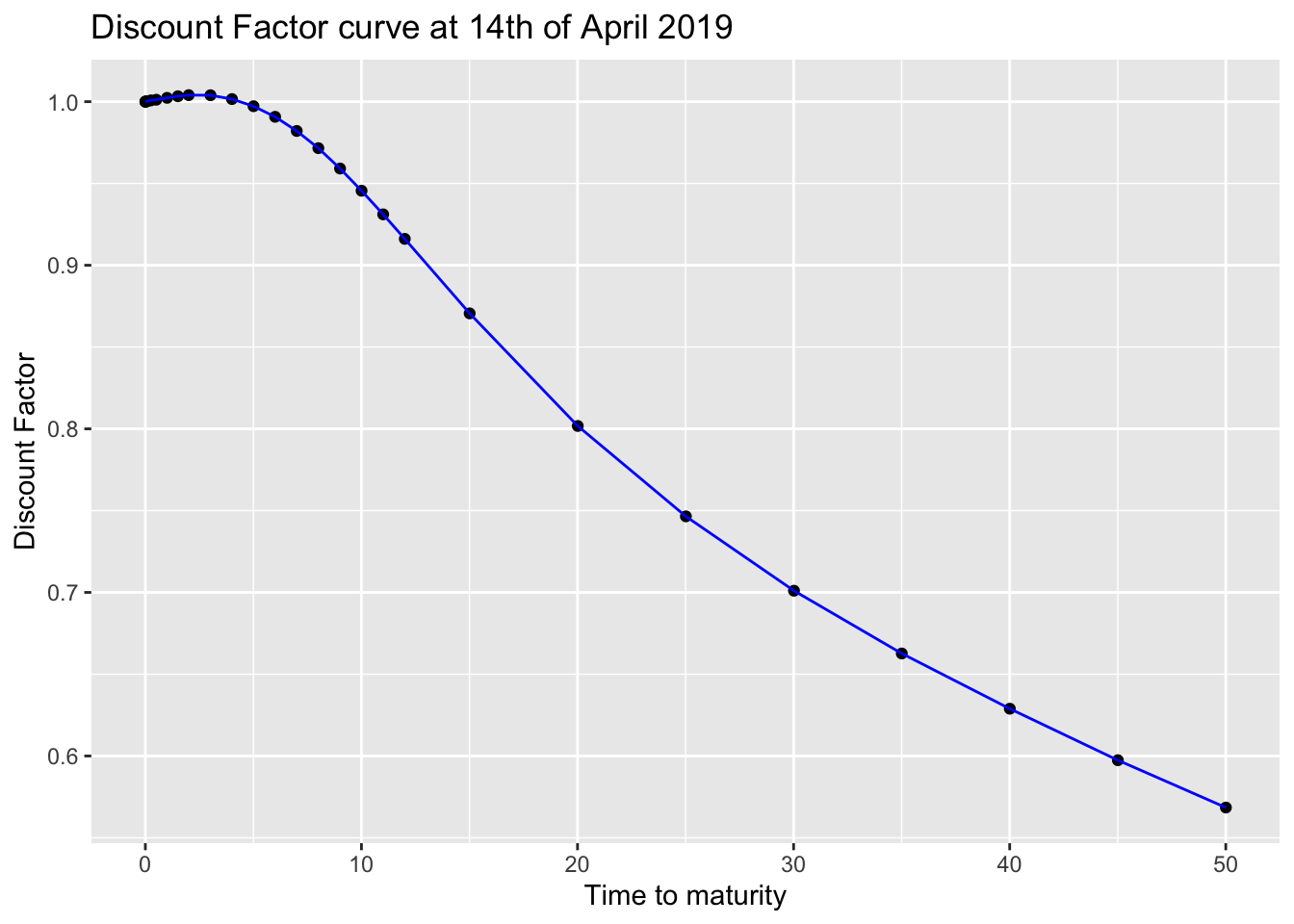
Interest Rate Swap pricing functions
I am now going to re-use the pricing functions that have been already described in a previous post. I have tidied them up a bit and given proper names, but the description still fully holds.
Let’s start from the one that calculates the swap cashflows.
SwapCashflowYFCalculation <- function(today, start.date, maturity.date,
time.unit, dcc, calendar) {
0:((lubridate::year(maturity.date) - lubridate::year(start.date)) *
(4 - time.unit)) %>%
purrr::map_dbl(~RQuantLib::advance(calendar = calendar,
dates = start.date,
n = .x,
timeUnit = time.unit,
bdc = 1,
emr = TRUE)) %>%
lubridate::as_date() %>%
{if (start.date < today) append(today, .) else .} %>%
purrr::map_dbl(~RQuantLib::yearFraction(today, .x, dcc)) %>%
tibble::tibble(yf = .)
}You may have noticed that I added one row {if (start.date < today) append(today, .) else .}. This allows to properly manage the pricing of swaps with a starting date before today.
I now proceed with calculating the actual par swap rate, which is a key input to the pricing formula. You can notice in the function below that I use a linear interpolation on the log of the discount factors. This is in line with one of the Bloomberg options. It is proven that it:
- provides step constant forward rates
- locally stabilises the bucketed sensitivities
Also the (old) swap rate pricing function is the same, we only filter for future cashflows as we want to be able to price swaps with a starting date before today.
OLDParSwapRate <- function(swap.cf){
swap.cf %<>%
dplyr::filter(yf >= 0)
num <- (swap.cf$df[1] - swap.cf$df[dim(swap.cf)[1]])
annuity <- (sum(diff(swap.cf$yf)*swap.cf$df[2:dim(swap.cf)[1]]))
return(list(swap.rate = num/annuity,
annuity = annuity))
}
ParSwapRateCalculation <- function(swap.cf.yf, df.table) {
swap.cf.yf %>%
dplyr::mutate(df = approx(df.table$t2m, log(df.table$df), .$yf) %>%
purrr::pluck("y") %>%
exp) %>%
OLDParSwapRate
}I now want to introduce two new functions which are needed for calculating the actual market values:
- the first one extracts the year fraction for the accrual calculation
the second one calculates the main characteristics of a swap:
- the par swap rate
- the pv01 (or analytic delta)
- the clean market value
- the accrual for the fixed rate leg
I have defined a variable direction which represents the type of swap:
- if it is equal to
1then it is a receiver swap - if it is equal to
-1then it is a payer swap
CalculateAccrual <- function(swap.cf){
swap.cf %>%
dplyr::filter(yf < 0) %>%
dplyr::select(yf) %>%
dplyr::arrange(dplyr::desc(yf)) %>%
dplyr::top_n(1) %>%
as.double %>%
{if (is.na(.)) 0 else .}
}
SwapCalculations <- function(swap.cf.yf, notional, strike, direction, df.table) {
swap.par.pricing <- ParSwapRateCalculation(swap.cf.yf, df.table)
mv <- notional * swap.par.pricing$annuity * (strike - swap.par.pricing$swap.rate) *
direction
accrual.fixed <- swap.cf.yf %>%
CalculateAccrual %>%
`*`(notional * strike * direction * -1)
pv01 <- notional/10000 * swap.par.pricing$annuity * direction
list(clean.mv = mv, accrual.fixed = accrual.fixed, par = swap.par.pricing$swap.rate,
pv01 = pv01)
}We then put everything together with the following pricing pipe:
SwapPricing <- function(today, swap, df.table) {
SwapCashflowYFCalculation(today, swap$start.date,
swap$maturity.date, swap$time.unit,
swap$dcc, swap$calendar) %>%
SwapCalculations(swap$notional, swap$strike, swap$direction, df.table)
}Pricing a swap
It’s showtime! :-) Let’s test our pricing function on a swap that we define as a list. This is a EUR 10m notional receiver swap starting on the 19th of January 2007 with 25 years of maturity. The paying dates are calculated using the modified following rule and the day count convention is 30/360.
swap.25y <- list(notional = 10000000,
start.date = lubridate::ymd(20070119),
maturity.date = lubridate::ymd(20320119),
strike = 0.00059820,
direction = 1,
time.unit = 3,
dcc = 6,
calendar = "TARGET")
SwapPricing(today, swap.25y, df.table)## $clean.mv
## [1] -881814.6
##
## $accrual.fixed
## [1] 1379.183
##
## $par
## [1] 0.007713252
##
## $pv01
## [1] 12393.65We can compare the results with the actual Bloomberg output:
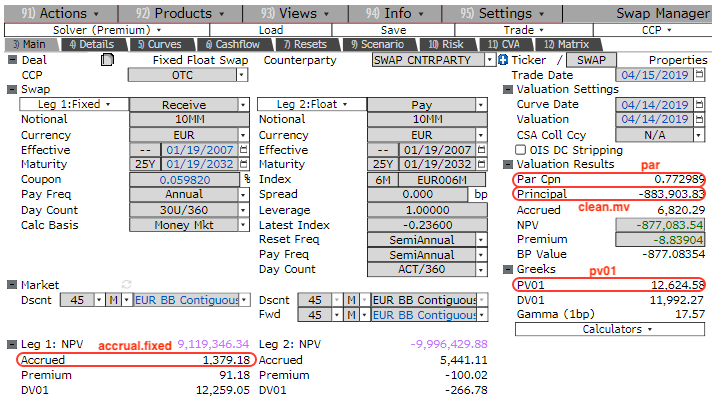
You can notice that:
- the par rate is exact to less than 1bp
- the clean market price difference is less than 0.2 dv01s
We can therefore say that the pricing functions have been validated.
Pricing a basket of swaps
With purrr it is very easy to vectorise the SwapPricing hence the pricing of a portfolio of swaps is seemingless.
I firstly have to define a number of different contracts, including a forward starting one.
I then combine all of them in a list and let the power of map.df do the magic.
swap.30y <- list(notional = 10000000,
start.date = lubridate::ymd(20120424),
maturity.date = lubridate::ymd(20420424),
strike = 0.01,
direction = -1,
time.unit = 3,
dcc = 6,
calendar = "TARGET")
swap.10y <- list(notional = 20000000,
start.date = lubridate::ymd(20120221),
maturity.date = lubridate::ymd(20220221),
strike = 0.0025,
direction = 1,
time.unit = 3,
dcc = 6,
calendar = "TARGET")
swap.2y.16y <- list(notional = 7500000,
start.date = lubridate::ymd(20210414),
maturity.date = lubridate::ymd(20370414),
strike = 0.015,
direction = 1,
time.unit = 3,
dcc = 6,
calendar = "TARGET")
swaps <- list(swap.25y = swap.25y, swap.30y = swap.30y, swap.10y = swap.10y,
swap.2y.16y = swap.2y.16y)
pricing.result <- swaps %>%
purrr::map_df(~SwapPricing(today, .x, df.table)) %>%
dplyr::mutate(swap.id = names(swaps)) %>%
dplyr::select(swap.id, dplyr::everything())| swap.id | clean.mv | accrual.fixed | par | pv01 |
|---|---|---|---|---|
| swap.25y | -881,814.61 | 1,379.18 | 0.77% | 12,393.65 |
| swap.30y | 233,691.75 | -97,222.22 | 1.11% | -20,867.00 |
| swap.10y | 222,083.28 | 7,361.11 | -0.14% | 5,724.42 |
| swap.2y.16y | 360,095.21 | -0.00 | 1.18% | 11,163.37 |
This is it for today. In the next post I will finish the pricing of this book of swaps calculating the accrual of the floating leg - which requires a bit of web scraping. Stay tuned.
